こちらの記事では、音を理解していく上で基礎となる音の種類と解析・分析方法についてまとめています。
音の種類
音の種類は大まかに分けて2つあります。
- 純音
- 複合音
これらについて詳細に見ていきましょう。
音の種類:純音
はじめに純音についてです。世の中で最も単純な音を純音と言います。
純音の波形は正弦波(sin波)で表すことができます。この音の性質は振幅と周波数の2つの要素によって決まります。振幅は圧力変化の最大値を示します。つまり、音の大きさに対応する要素です。また、周波数は1秒あたりに振幅する回数を示す要素です。よって、音の高さに対応している要素です。
音の種類:複合音
複合音は、純音が複数重なった音のことを指します。人間の声や楽器の音など、日常的に接する音は大抵複合音に分類されます。
複合音の波形は大抵非常に複雑なものであり、簡単な数式で表すことは困難です。よって、複合音のような複雑な音を解析するには、周波数解析(=フーリエ解析)や周波数分析を利用します。
音の分析方法
音の分析方法はいくつかあります。
- 周波数解析(フーリエ解析)
- 周波数分析
ここでは代表的な周波数解析について紹介します。
音の分析方法:周波数解析(フーリエ解析)
はじめに周波数解析からです。周波数解析とは、光や音等の波を分解して分析する手法です。
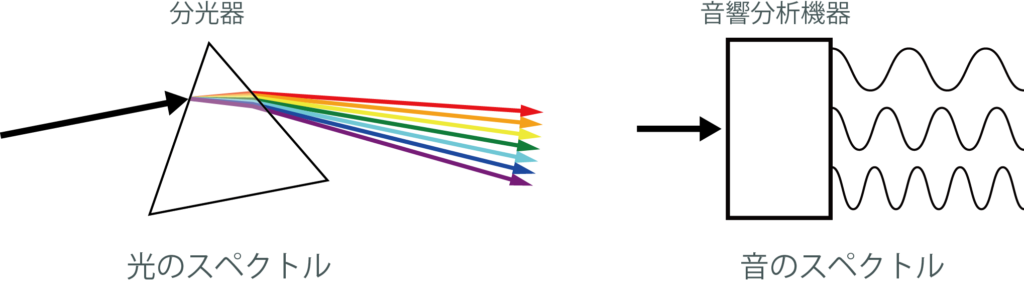
光のスペクトルは光の色ごとの周波数(振動数)の違いを利用して分解された色の分布です。これと同様に、複合音も音響分析機器で周波数ごとに音を分解することができ、それを利用して音を解析する手法が周波数解析です。フーリエ解析を応用した解析方法です。
フーリエ(ジョセフ・フーリエ)・フーリエ解析とは
フーリエとは、フランスの数学・物理学者です。周波数解析を行う上で重要な理論であるフーリエ展開やフーリエ変換を提唱した人物です。
フーリエ展開・フーリエ変換とは、有限区間上あるいは無限区間の関数を三角関数の級数で表すことです。これらの理論を用いて関数を解析すること、特に関数を周波数成分に分解して調べるものをフーリエ解析と言います。
周波数分析を行う流れとしては、下の画像のようなイメージです。
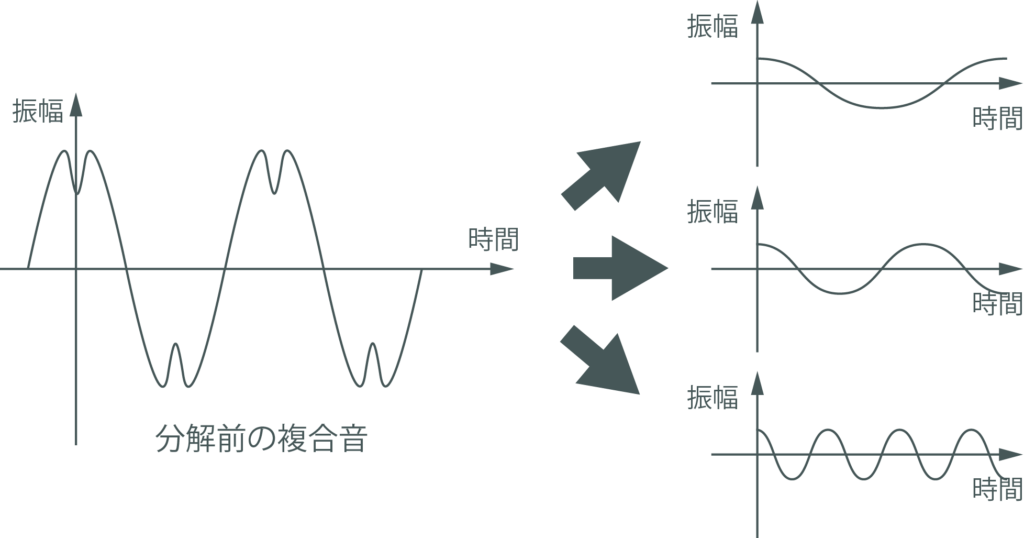
まとめ
こちらの記事では、音の種類(純音・複合音)と音の分析方法の一つである周波数分析(フーリエ解析)を紹介しました。これらはどれも音の基礎となる重要な知識ですので、ぜひ覚えておきましょう。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。


